Grafika Komputer : Algoritma Klipping (Clipping ) - Pertemuan 11

-

Pertemuan 11

ALGORITMA KLIPPING
( CLIPPING )

Clipping
⚫ Clipping adalah metoda untuk hanya menampilkan garis pada area yang visible (terlihat)


Visible dan Invisible Line
⚫ Berdasarkan posisi garis terhadap area gambar maka garis dapat dibedakan menjadi :

⚫ Bagaimana menentukan visible dan invisible line? 
    ⚫ fully visible :  (x1 ≥ xmin) dan (x1 ≤ xmax) dan (y1 ≥ ymin) dan (y1 ≤ ymax) dan (x2 ≥ xmin) dan                                    (x2 ≤ xmax) dan (y2 ≥ ymin) dan (y2 ≤ ymax) 
    ⚫ partially visible : -- coba sendiri dan anda akan menemukan bahwa tidak mudah melakukan hal                                                 tersebut ! --

Algorithma Clipping
⚫ Berbagai algorithma telah dikembangkan untuk menangani masalah pemotongan garis tersebut,              antara lain : 
                                        ⚫ Cyrus-Beck 
                                        ⚫ Cohen-Sutherland

Algorithma Cohen-Sutherland
⚫ Area gambar dibatasi oleh xmin,xmax, ymin,ymax
⚫ Cohen dan Sutherland memberikan kode kepada tiap area yang mungkin dilewati oleh sebuah garis       atau disebut sebagai region code. 
⚫ Region code mempunyai panjang empat bit dan menggunakan urutan sebagai berikut :
T(op) = 1 jika ujung garis berada di atas area gambar selain itu 0 (nol) 
B(ottom)  = 1 jika ujung garis berada di bawah area gambar selain itu 0 (nol) 
L(eft) = 1 jika ujung garis berada di kiri area gambar selain itu 0 (nol) 
R(ight) = 1 jika ujung garis berada di kanan area gambar selain itu 0 (nol)

⚫ Sehingga diperoleh region code :


⚫ Garis kemungkinan partially visible atau fully invisible apabila region code dari ujung garis tersebut       mempunyai bit bernilai 1
⚫ Pemotongan (clipping) dilakukan terhadap ujung-ujung garis yang region code berisi bit bernilai 1. ⚫ Contoh sebelumnya menunjukkan bahwa ujung Pa, Pb, Qc,Qd dan Re yang akan mengalami                 pemotongan.



⚫ Dengan menggunakan cara yang sama maka lokasi titik potong untuk tiap area akan sesuai tabel di       bawah ini :
⚫ Koordinat titik potong dapat dicari dengan cara :


⚫ Contoh 
    • Diketahui : area gambar : (1,2)-(5,5) 
    • Ditanyakan : 
                            ⚫ lokasi titik potong dari garis P (2,1) - (4,6) terhadap area gambar 
                            ⚫ lokasi titik potong dari garis S (2,6) - (6,3)





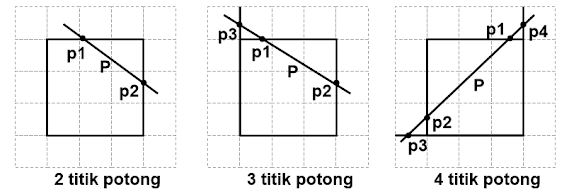
⚫ Untuk ujung-ujung garis dengan region code berisi bit 1 maka ada tiga kemungkinan perpotongan          antara garis P dengan area gambar



⚫ Apabila ditemukan lebih dari satu titik potong maka pilih titik potong yang paling "dekat" dengan         area gambar. 
⚫ Bagaimana pengertian "dekat" didefinisikan? 
        ⚫ Tugas anda mendefinisikan pengertian "dekat" tersebut!

⚫ Algorithma Cohen-Sutherland dapat dituliskan sebagai berikut :

Ambil ujung pertama (Pa) dari garis P 
rc = Tentukan Region Code dari Pa 
switch (rc)
0 : p  = Pa  
1 : p  = (xmin,yp1) 
2 : p  = (xmax,yp2) 
4 : p  = (xp2,ymin) 
5 : p1 = (xp2,ymin) ; p2 = (xmin,yp1) 
    Tentukan mana yang lebih dekat antara p1 & p2 
6 : p1 = (xp2,ymin) ; p2 = (xmax,yp2) 
    p  = Tentukan mana yang lebih dekat antara p1 & p2 
8 : p  = (xp1,ymax) 
9 : p1 = (xp1,ymax) ; p2 = (xmin,yp1) 
    p  = Tentukan mana yang lebih dekat antara p1 & p2 
10 : p1 = (xp2,ymax) ; p2 = (xmin,yp1) 
    p  = Tentukan mana yang lebih dekat antara p1 & p2

Ambil ujung kedua (Pb) dari garis P 
rc = Tentukan Region Code dari Pb 
switch (rc) 
0 : q  = Pb  
1 : q  = (xmin,yp1) 
2 : q  = (xmax,yp2) 
4 : q  = (xp2,ymin) 
5 : p1 = (xp2,ymin) ; p2 = (xmin,yp1) 
    q  = Tentukan mana yang lebih dekat antara p1 & p2 
6 : p1 = (xp2,ymin) ; p2 = (xmax,yp2) 
    q  = Tentukan mana yang lebih dekat antara p1 & p2 
8 : p1 = (xp1,ymax) 
9 : p1 = (xp1,ymax) ; p2 = (xmin,yp1) 
    q  = Tentukan mana yang lebih dekat antara p1 & p2 
10 : p1 = (xp2,ymax) ; p2 = (xmin,yp1) 
    q  = Tentukan mana yang lebih dekat antara p1 & p2 
        Gambar garis dari p menuju q

Komentar

Posting Komentar

Postingan populer dari blog ini

Grafika Komputer : PROYEKSI - Pertemuan 12

-
Gambar
    Pertemuan 12 PROYEKSI PROYEKSI ◼ Proyeksi adalah metoda menggambarkan benda tiga dimensi pada bidang 2 dimensi.  ◼ Ada 2 cara melakukan proyeksi :  ❑ Proyeksi paralel : Semua garis paralel akan tampak paralel pada bidang proyeksi.  ❑ Proyeksi perspektif : Semua garis paralel akan menghilang di titik pusat proyeksi. PROYEKSI PARALEL ◼ Ada dua macam proyeksi paralel :  ❑ Proyeksi Orthographic  ❑ Proyeksi Oblique  ◼ Proyeksi orthographic adalah proyeksi dengan mata tegak lurus terhadap bidang proyeksi. ◼ Proyeksi Oblique adalah proyeksi dengan mata berada di lokasi yang tidak tegak lurus terhadap bidang proyeksi. PROYEKSI ORTHOGRAPHIC ◼ Proyeksi orthographic dibagi menjadi 2 macam :  ❑ Pandangan Multiview Orthographic  ❑ Pandangan Axonometric yang dibagi menjadi tiga macam :       ◼ Isometric : Proyeksi dimana 3 muka dipendekkan dalam ukuran yang sama       ◼ Dimetric : Proyeksi dimana 2 muka benda dipendekkan dalam ukuran yang sama       ◼ Trimetric : Proyeksi dimana 2 muka dipendek
Baca selengkapnya

Grafika Komputer : DUNIA 3 DIMENSI - Pertemuan 13

-
Gambar
    Pertemuan 13 DUNIA 3 DIMENSI 2 Dimensi dan 3 DIMENSI ◼ Apa yang membedakan 2 dimensi dengan 3 dimensi ?  ❑ 2 Dimensi : Tinggi dan Lebar  ❑ 3 Dimensi : Tinggi, Lebar dan Kedalaman  ◼ Kedalaman adalah jarak antara pemirsa (viewer) terhadap benda yang dia lihat 3 Dimensi ◼ Bagaimana manusia memperoleh kesan kedalaman ?  ❑ Manusia mempunyai dua mata.  ❑ Kedua mata manusia mempunyai selisih sudut pandang 120o  ❑ Perbedaan sudut pandang tersebut membuat masing-masing mata memperoleh gambar yang berbeda untuk objek yang sama.  ❑ Perbedaan gambar diproses oleh otak sehingga kita memperoleh kesan 'kedalaman' atau jarak terhadap benda.  ◼ Percobaan : Tutup salah satu mata anda selama kurang lebih 2 hari dan anda akan mengetahui bahwa anda tidak dapat menentukan dengan mudah jarak antara anda dengan benda yang anda lihat. Sifat-sifat 3 dimensi ◼ Setiap titik dalam 3 dimensi ditentukan oleh tiga posisi :  ❑ x : jarak titik tersebut terhadap sumbu x  ❑ y : jarak titik tersebut terhadap
Baca selengkapnya

Grafika Komputer : TRANSFORMASI 2 DIMENSI - Pertemuan 10

-
Gambar
  Pertemuan 10 TRANSFORMASI 2 DIMENSI TRANSFORMASI ◼ Metoda untuk memanipulasi lokasi sebuah titik. ◼ Ada 3 macam transformasi : ❑ Translation (Pergerseran) ❑ Scaling (Penskalaan) ❑ Rotation (Pemutaran) TRANSLATION ◼ Titik A (x,y) digeser sejumlah Trx pada sumbu x dan digeser sejumlah Try pada sumbu y ◼ Rumus Umum : Q(x,y) = P(x,y) +Tr = P(x+Trx, y+Try) ◼Contoh : Diketahui : A(2,4) digesersejauh (4,2) Ditanya : lokasi hasil pergeseran (A’) Jawab : A’ (x,y) = A + Tr = (2,4) + (4,2) = (6,6) SCALING ◼ Menggunakan asumsi titik pusat (0,0) ◼ Lokasi asli dikalikan dengan besaran Sx pada sumbu x dan Sy pada sumbu y ◼ Rumus Umum : Q(x,y) = A * S = A(x,y) * S(x,y) = A(x*Sx, y * Sy) CONTOH Diketahui : Titik A (1,1); B(3,1); C(2,2), ketiga titik tersebut diskalakan sebesar Sx = 2 dan Sy = 3 Ditanyakan : Lokasi titik hasil penskalaan Jawab : A’=(1*2, 1*3) = (2,3) B’=(3*2, 1*3) = (6,3) C’=(2*2, 2*3) = (4,6) ROTASI ◼ Perhatikan gambar di bawah ini : ROTATION Diketahui : A(1,1);B(3,1);C(2,2) Ditanyak
Baca selengkapnya